第1行:
第1行:
{{noteTA|G1=物理學}}
{{noteTA|G1=物理學}}
[[File:Flight_dynamics_with_text.png|thumb|200px|right|刚体的空间组态决定于其[[质心]]位置与其[[定向(幾何)|定向]](最少有六个参数)。<ref name=Sciavicco>
[[File:Flight_dynamics_with_text.png|thumb|200px|right|刚体的空间组态决定于其[[质心]]位置与其[[定向 (幾何)|定向]](最少有六个参数)。<ref name=Sciavicco>
{{cite book |title=Modelling and control of robot manipulators |author=Lorenzo Sciavicco, Bruno Siciliano |chapter=§2.4.2 Roll-pitch-yaw angles |page=32 |isbn=1852332212 |year=2000 |edition=2nd |publisher=Springer}}
{{cite book |title=Modelling and control of robot manipulators |author=Lorenzo Sciavicco, Bruno Siciliano |chapter=§2.4.2 Roll-pitch-yaw angles |page=32 |isbn=1852332212 |year=2000 |edition=2nd |publisher=Springer}}
</ref>]]
</ref>]]
第67行:
第67行:
方向餘弦矩陣 <math>A</math> 足以設定附體參考系B的定向。但是,矩陣 <math>A</math> 有九個元素,而剛體只能供給三個自由度來做定向,因為這九個元素不是[[自變量]]({{lang|en|independent variable}}))。歐拉角的三個自變量可以用來設定剛體的定向。
方向餘弦矩陣 <math>A</math> 足以設定附體參考系B的定向。但是,矩陣 <math>A</math> 有九個元素,而剛體只能供給三個自由度來做定向,因為這九個元素不是[[自變量]]({{lang|en|independent variable}}))。歐拉角的三個自變量可以用來設定剛體的定向。
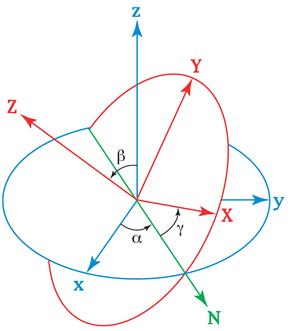
相對於空間參考系S,附體參考系B的定向,可以用三個歐拉角來設定。參閲右圖。設定 xyz-軸為空間參考系S的坐標軸,XYZ-軸為附體參考系B的坐標軸。稱 xy-平面與 XY-平面的相交為'''交點線''',用英文字母(N)代表。按照「zxz 順規」,歐拉角可以這樣定義:
相對於空間參考系S,附體參考系B的定向,可以用三個歐拉角來設定。參閱 右圖。設定 xyz-軸為空間參考系S的坐標軸,XYZ-軸為附體參考系B的坐標軸。稱 xy-平面與 XY-平面的相交為'''交點線''',用英文字母(N)代表。按照「zxz 順規」,歐拉角可以這樣定義:
*<math>\alpha</math> 是 x-軸與交點線之間的夾角,
*<math>\alpha</math> 是 x-軸與交點線之間的夾角,
*<math>\beta</math> 是 z-軸與Z-軸之間的夾角,
*<math>\beta</math> 是 z-軸與Z-軸之間的夾角,
第90行:
第90行:
單獨分開工作,每個矩陣各自代表一種旋轉。按照順序相乘,
單獨分開工作,每個矩陣各自代表一種旋轉。按照順序相乘,
* 最裏面的(最右的) 矩陣代表繞著 z 軸的旋轉。
* 最裏面的( 最右的) 矩陣代表繞著 z 軸的旋轉。
* 最外面的(最左的) 矩陣代表繞著 Z 軸的旋轉。
* 最外面的( 最左的) 矩陣代表繞著 Z 軸的旋轉。
* 在中間的矩陣代表繞著交點線的旋轉。
* 在中間的矩陣代表繞著交點線的旋轉。
第111行:
第111行:
[[歐拉旋轉定理]]表明,在三維空間裏,假設約束剛體內部一點固定不動,則其任意位移等價於繞著某固定軸的一個旋轉,而這固定軸必含有這固定點。換句話說,設定附體參考系B的原點為這固定點,則附體參考系B不會因為這位移而涉及任何平移運動,再設定附體參考系B的z-軸與固定軸同軸,則這位移對應於繞著附體參考系B的z-軸旋轉 <math>\gamma</math> 角弧,而z-軸的方向是由 <math>\alpha</math> 與 <math>\beta</math> 角弧給出。<ref name=Whittaker_1917>{{cite book|last=Whittaker|first=Edmund |title=A treatise on the analytical dynamics of particles and rigid bodies; with an introduction to the problem of three bodies |publisher=Cambridge University Press|pages=2-5|date=1917|url= http://www.archive.org/details/cu31924001080294}}</ref>
[[歐拉旋轉定理]]表明,在三維空間裏,假設約束剛體內部一點固定不動,則其任意位移等價於繞著某固定軸的一個旋轉,而這固定軸必含有這固定點。換句話說,設定附體參考系B的原點為這固定點,則附體參考系B不會因為這位移而涉及任何平移運動,再設定附體參考系B的z-軸與固定軸同軸,則這位移對應於繞著附體參考系B的z-軸旋轉 <math>\gamma</math> 角弧,而z-軸的方向是由 <math>\alpha</math> 與 <math>\beta</math> 角弧給出。<ref name=Whittaker_1917>{{cite book|last=Whittaker|first=Edmund |title=A treatise on the analytical dynamics of particles and rigid bodies; with an introduction to the problem of three bodies |publisher=Cambridge University Press|pages=2-5|date=1917|url= http://www.archive.org/details/cu31924001080294}}</ref>
[[Image:Change of axes.svg|thumb|right|200px|改變剛體的定向與旋轉其附體參考系相同。]]
對於內部有一點被約束固定不動的剛體(或原點固定不動的參考系),歐拉旋轉定理將其任意位移等價為繞著某固定軸的一個旋轉。這允許使用旋轉來表達定向的改變。因此,變換矩陣 <math>A</math> 可以視為[[旋转矩阵#三维空间|三維旋轉]]的[[旋轉矩陣]],將附體參考系B或剛體做任意環繞著固定點的旋轉,從 <math>\hat{\mathbf{e}}_1</math> 、<math>\hat{\mathbf{e}}_2</math> 、<math>\hat{\mathbf{e}}_3</math> 旋轉成為 <math>\hat{\mathbf{e}}'_1</math> 、<math>\hat{\mathbf{e}}'_2</math> 、<math>\hat{\mathbf{e}}'_3</math> 。參考軸 <math>\hat{\mathbf{e}}'_i</math> 與 <math>\hat{\mathbf{e}}_j</math> 之間的關係為
對於內部有一點被約束固定不動的剛體(或原點固定不動的參考系),歐拉旋轉定理將其任意位移等價為繞著某固定軸的一個旋轉。這允許使用旋轉來表達定向的改變。因此,變換矩陣 <math>A</math> 可以視為[[旋转矩阵#三维空间|三維旋轉]]的[[旋轉矩陣]],將附體參考系B或剛體做任意環繞著固定點的旋轉,從 <math>\hat{\mathbf{e}}_1</math> 、<math>\hat{\mathbf{e}}_2</math> 、<math>\hat{\mathbf{e}}_3</math> 旋轉成為 <math>\hat{\mathbf{e}}'_1</math> 、<math>\hat{\mathbf{e}}'_2</math> 、<math>\hat{\mathbf{e}}'_3</math> 。參考軸 <math>\hat{\mathbf{e}}'_i</math> 與 <math>\hat{\mathbf{e}}_j</math> 之間的關係為
:<math>\hat{\mathbf{e}}'_i=a_{ij}\hat{\mathbf{e}}_j</math> 。
:<math>\hat{\mathbf{e}}'_i=a_{ij}\hat{\mathbf{e}}_j</math> 。
第120行:
第121行:
其中,<math>\mathbf{r}_{G}</math> 、<math>\mathbf{r}_{P/G}</math> 分別是點G的位置、從點G到點P的位移。
其中,<math>\mathbf{r}_{G}</math> 、<math>\mathbf{r}_{P/G}</math> 分別是點G的位置、從點G到點P的位移。
⚫ 從附體參考系B觀測,剛體內部每一點的位置都固定不變。剛體從時間 <math>t_0</math> 到時間 <math>t</math> 的運動,可以分為點G從 <math>\mathbf{r}_{G}(t_0)</math> 到 <math>\mathbf{r}_{G}(t)</math> 的平移運動,與位移 <math>\mathbf{r}_{P/G}</math> 從時間 <math>t_0</math> 到時間 <math>t</math> 的旋轉運動。
⚫ <math>\mathbf{
r}_{P/G}</math>
可以分解為
:<math>\mathbf{r}_{P/G}=x_1\hat{\mathbf{x}}_1+x_2\hat{\mathbf{x}}_2+x_3\hat{\mathbf{x}}_3=e_1\hat{\mathbf{e}}_1+e_2\hat{\mathbf{e}}_2+e_3\hat{\mathbf{e}}_3</math> ,
⚫ 從附體參考系B觀測,剛體內部每一點的位置都固定不變
,所以,<math>(e_1,e_2,e_3)</math> 是常向量。剛體從時間 <math>t_0</math> 到時間 <math>t</math> 的運動,可以分為點G從 <math>\mathbf{r}_{G}(t_0)</math> 到 <math>\mathbf{r}_{G}(t)</math> 的平移運動,與位移 <math>\mathbf{r}_{P/G}</math> 從時間 <math>t_0</math> 到時間 <math>t</math> 的旋轉運動。
===平移速度與角速度===
===平移速度與角速度===
從不同的參考系觀測,剛體運動的平移速度與角速度是從某參考系可能不同,為了確保測量結果具有實際物理意義,必需先設定參考系。
從不同的參考系觀測剛體運動,可能會獲得不同 的平移速度和不同的 角速度。 為了確保測量結果具有實際物理意義,必需先給 定參考系。
剛體的平移速度是向量,是其位置向量的時間變化率,是附著於剛體的附體參考系的原點的速度。對於純平移運動(沒有任何旋轉運動),剛體內部所有點的移動速度相同。假設涉及旋轉運動,則通常剛體內部任意兩點的瞬時速度不相等;只有當它們恰巧處於同一直軸,而這直軸平行於[[轉動瞬軸]]({{lang|en|instantaneous axis of rotation}}),則它們的瞬時速度相等。
剛體的平移速度是向量,是其位置向量的時間變化率,是附著於剛體的附體參考系的原點的速度。對於純平移運動(沒有任何旋轉運動),剛體內部所有點的移動速度相同。假設涉及旋轉運動,則通常剛體內部任意兩點的瞬時速度不相等;只有當它們恰巧處於同一直軸,而這直軸平行於[[轉動瞬軸]]({{lang|en|instantaneous axis of rotation}}),則它們的瞬時速度相等。
角速度也是向量,描述剛體定向改變的角速率,以及剛體旋轉時的瞬時轉軸([[歐拉旋轉定理]]保證瞬時轉軸的存在)。在任意時間,剛體內部每一個粒子的角速度相同。
角速度也是向量,描述剛體定向改變的角速率,以及剛體旋轉時的瞬時轉軸([[歐拉旋轉定理]]保證瞬時轉軸的存在)。在任意時間,剛體內部每一個粒子的角速度相同。
====向量的時間變化率====
假設一剛體呈純旋轉運動,其附體參考系B也會跟著旋轉,因此,對於任意向量 <math>\mathbf{F}</math> ,從這附體參考系B與從空間參考系S觀測,會得到不同的結果。假設附體參考系B <math>(\hat{\mathbf{e}}_1,\hat{\mathbf{e}}_2,\hat{\mathbf{e}}_3)</math> 與空間參考系S <math>(\hat{\mathbf{x}}_1,\hat{\mathbf{x}}_2,\hat{\mathbf{x}}_3)</math> 同原點。對於這些參考系,三維含時向量 <math>\mathbf{F}(t)</math> 分解為
:<math>\mathbf{F}=f_i\hat{\mathbf{x}}_i=F_i\hat{\mathbf{e}}_i</math> 。
⚫ <math>\mathbf{
F }
(t) </math>
對於時間的導數 為
:<math>\frac{\mathrm{d}\mathbf{F}}{\mathrm{d}t}=\frac{\mathrm{d}f_i}{\mathrm{d}t}\hat{\mathbf{x}}_i=\frac{\mathrm{d}F_i}{\mathrm{d}t}\hat{\mathbf{e}}_i+F_i\frac{\mathrm{d}\hat{\mathbf{e}}_i}{\mathrm{d}t}</math> 。
單獨計算附體參考軸對於時間的導數:
:<math>\frac{\mathrm{d}\hat{\mathbf{e}}_i}{\mathrm{d}t}
=\frac{\mathrm{d}}{\mathrm{d}t}(a_{ij}\hat{\mathbf{x}}_j)
=\dot{a}_{ij}\hat{\mathbf{x}}_j
=\dot{a}_{ij}a_{kj}\hat{\mathbf{e}}_k</math> ;
其中,<math>\dot{a}_{ij}\ \stackrel{def}{=}\ \frac{\mathrm{d}}{\mathrm{d}t}a_{ij}</math> 是方向餘弦對於時間的導數。
由於 <math>\frac{\mathrm{d}}{\mathrm{d}t}\hat{\mathbf{e}}_i</math> 垂直於 <math>\hat{\mathbf{e}}_i</math> ,<math>\frac{\mathrm{d}}{\mathrm{d}t}\hat{\mathbf{e}}_i</math> 只能是其他兩個單位向量的[[線性組合]]:
:<math>\frac{\mathrm{d}}{\mathrm{d}t}\hat{\mathbf{e}}_i=-\epsilon_{ij\ell}\omega_{ij}\hat{\mathbf{e}}_{\ell}</math> ;
其中,<math>\epsilon_{ij\ell}</math> 是[[列維-奇維塔符號]],<math>\omega_{ij}</math> 是係數。
對於任意 <math>\hat{\mathbf{e}}_{m}\ne \hat{\mathbf{e}}_i</math> ,
單位向量 <math>\hat{\mathbf{e}}_i</math> 與 <math>\hat{\mathbf{e}}_{m}</math> 的內積對於時間的導數為
:<math>\begin{align}\frac{\mathrm{d}}{\mathrm{d}t}(\hat{\mathbf{e}}_{i}\cdot\hat{\mathbf{e}}_{m}) & =\left(\frac{\mathrm{d}}{\mathrm{d}t}\hat{\mathbf{e}}_{i}\right) \cdot\hat{\mathbf{e}}_{m}
+\hat{\mathbf{e}}_{i}\cdot\left(\frac{\mathrm{d}}{\mathrm{d}t}\hat{\mathbf{e}}_{m}\right) \\
& =-\epsilon_{ij\ell}\omega_{ij}\hat{\mathbf{e}}_{\ell} \cdot\hat{\mathbf{e}}_{m}
-\hat{\mathbf{e}}_{i} \cdot\epsilon_{mj\ell}\omega_{mj}\hat{\mathbf{e}}_{\ell} \\
& =-\epsilon_{ijm}\omega_{ij}-\epsilon_{mji}\omega_{mj} \\
& =-\epsilon_{ijm}(\omega_{ij}-\omega_{mj}) \\
& =0 \\
\end{align}</math>
所以, <math>\omega_{ij}</math> 的下標 <math>i</math> 多餘無用,可以刪除,變為 <math>\omega_{j}</math> :
:<math>\frac{\mathrm{d}}{\mathrm{d}t}\hat{\mathbf{e}}_i=-\epsilon_{ij\ell}\omega_{j}\hat{\mathbf{e}}_{\ell} </math> 。
思考 <math>\frac{\mathrm{d}\mathbf{F}}{\mathrm{d}t}</math> 方程式最右邊項目 <math>F_i\frac{\mathrm{d}\hat{\mathbf{e}}_i}{\mathrm{d}t}</math> ,對換傀標 <math>i</math> <math>\ell</math> ,可以得到
:<math>F_i\frac{\mathrm{d}\hat{\mathbf{e}}_i}{\mathrm{d}t}
=-\epsilon_{ij\ell}F_i\omega_{j}\hat{\mathbf{e}}_{\ell}
=\epsilon_{ij\ell}\hat{\mathbf{e}}_{i}\omega_{j}F_{\ell}
=\boldsymbol{\omega}\times\mathbf{F}</math> 。
向量 <math>\boldsymbol{\omega}</math> 是由三個係數 <math>\omega_1</math> 、<math>\omega_2</math> 、<math>\omega_3</math> 組成,對應於附體參考系的三個參考軸 <math>\hat{\mathbf{e}}_1</math> 、<math>\hat{\mathbf{e}}_2</math> 、<math>\hat{\mathbf{e}}_3</math> ,係數數值可以從歐拉角計算求得:
:<math>\omega_1=\dot{a}_{2j}a_{3j}
=\dot{\alpha}\sin{\beta}\sin{\gamma}+\dot{\beta}\cos{\gamma}</math> 、
:<math>\omega_2=-\dot{a}_{1j}a_{3j}
=\dot{\alpha}\sin{\beta}\cos{\gamma}+\dot{\beta}\sin{\gamma}</math> 、
:<math>\omega_3=\dot{a}_{1j}a_{2j}=\dot{\alpha}\cos{\beta}+\dot{\gamma}</math> 。
試想對應於歐拉角 <math>\alpha</math> 、<math>\beta</math> 、<math>\gamma</math> 的三個旋轉軸分別為 <math>\hat{\mathbf{z}}</math> 、<math>\hat{\mathbf{N}}</math> 、<math>\hat{\mathbf{Z}}</math> ,三個角速度分別為
:<math>\boldsymbol{\omega}_{\alpha}=\dot{\alpha}\hat{\mathbf{z}}
=\dot{\alpha}\sin{\beta}\sin{\gamma}\hat{\mathbf{X}}+\dot{\alpha}\sin{\beta}\cos{\gamma}\hat{\mathbf{Y}}+\dot{\alpha}\cos{\beta}\hat{\mathbf{Z}}
</math> 、
:<math>\boldsymbol{\omega}_{\beta}=\dot{\beta}\hat{\mathbf{N}}
=\dot{\beta}\cos{\gamma}\hat{\mathbf{X}}-\dot{\beta}\sin{\gamma}\hat{\mathbf{Y}}
</math> 、
:<math>\boldsymbol{\omega}_{\gamma}=\dot{\gamma}\hat{\mathbf{Z}}</math> 。
這三個角速度的向量和,對於附體參考系B的分量分別為
:<math>\omega_X=\dot{\alpha}\sin{\beta}\sin{\gamma}+\dot{\beta}\cos{\gamma}=\omega_1</math> 、
:<math>\omega_Y=\dot{\alpha}\sin{\beta}\cos{\gamma}+\dot{\beta}\sin{\gamma}=\omega_2</math> 、
:<math>\omega_Z=\dot{\alpha}\cos{\beta}+\dot{\gamma}=\omega_3</math> 。
注意到附體參考系B的 <math>\hat{\mathbf{e}}_1</math> 、<math>\hat{\mathbf{e}}_2</math> 、<math>\hat{\mathbf{e}}_3</math> 就是歐拉角的 <math>\hat{\mathbf{X}}</math> 、<math>\hat{\mathbf{Y}}</math> 、<math>\hat{\mathbf{Z}}</math> ,所以,向量 <math>\boldsymbol{\omega}</math> 是附體參考系B旋轉的角速度。
總結,向量 <math>\mathbf{F}(t)</math> 對於時間的導數為
:<math>\frac{\mathrm{d}\mathbf{F}}{\mathrm{d}t}=\frac{\mathrm{d}f_i}{\mathrm{d}t}\hat{\mathbf{x}}_i=\frac{\mathrm{d}F_i}{\mathrm{d}t}\hat{\mathbf{e}}_i+\boldsymbol{\omega}\times\mathbf{F}</math> 。
設定 <math>\left(\frac{\mathrm{d}\mathbf{F}}{\mathrm{d}t}\right)_{\mathrm{space}}</math> 、<math>\left(\frac{\mathrm{d}\mathbf{F}}{\mathrm{d}t}\right)_{\mathrm{body}}</math> 分別為從空間參考系S、附體參考系B觀測到的向量 <math>\mathbf{F}(t)</math> 對於時間的導數,上述方程式可以表達為
:<math>\left(\frac{\mathrm{d}\mathbf{F}}{\mathrm{d}t}\right)_{\mathrm{space}}=\left(\frac{\mathrm{d}\mathbf{F}}{\mathrm{d}t}\right)_{\mathrm{body}}+\boldsymbol{\omega}\times\mathbf{F}</math> 。
由於向量 <math>\mathbf{F}(t)</math> 是任意向量,可以將 <math>\left(\frac{\mathrm{d}}{\mathrm{d}t}\right)_{\mathrm{space}}</math> 、<math>\left(\frac{\mathrm{d}}{\mathrm{d}t}\right)_{\mathrm{body}}</math> 當作算符,這樣,對應的算符方程式的形式為:
:<math>\left(\frac{\mathrm{d}}{\mathrm{d}t}\right)_{\mathrm{space}}=\left(\frac{\mathrm{d}}{\mathrm{d}t}\right)_{\mathrm{body}}+\boldsymbol{\omega}\times</math> 。
這算符方程式可以作用於任意含時向量。
==动力学==
==动力学==
刚体的空间组态决定于其质心 位置与其定向 (最少有六个参数)。[ 1] 在物理学 裏,理想刚体 (rigid body )是一種有限尺寸,可以忽略形变 的固体 。不论是否感受到外力 ,在刚体內部,点 与点之间的距离 都不会改变。根據相對論 ,這種物體不可能實際存在,但物體通常可以假定為完美剛體,前提是必須滿足運動速度超小於光速 的條件。
在经典力学 裡,刚体通常被认为是连续质量分佈体;在量子力学 裏,刚体被認為是一群粒子的聚集。例如,分子 (由假定為質點 的电子 与核子 组成)时常會被视为刚体(請参阅條目分子的分类为刚性转子 (classification of molecules as rigid rotors ))。
剛體是由一群數量超多的粒子組成。實際而言,不可能精確地追蹤其中每一個粒子的運動。為了簡化運算,可以利用剛體的剛性,即其內部所有粒子彼此之間距離不變的性質。假若物體具有剛性,則倚靠設定三個不同線粒子的位置,就足以設定此物體的位置。這意味著,在三維空間裏,剛體至多只有九個自由度 ,但由於假定三個粒子之間的距離固定不變,所以,剛體只有六個自由度。假設還有其它約束,例如,剛體的運動必需繞著其內部一點旋轉,或繞著其內部一直軸旋轉,則自由度會小於六。
關於其它任意粒子P的位置,只要知道粒子P與上述三個粒子之中的任意一個粒子的相對位置,就可以重建這粒子的位置。通常,整個剛體的空間組態可以簡易地以以下參數設定:
剛體的「位置」:挑選剛體內部一點G來代表整個剛體,通常會設定物體的質心 或形心 為這一點。從空間參考系S觀測,點G的位置就是整個剛體在空間的位置。表示位置可以應用向量的概念。向量的起點為參考系S的原點,終點為點G。設定剛體的位置需要三個坐標,例如,採用直角坐標系 ,這三個坐標為x-坐標、y-坐標、z-坐標。這用掉了三個自由度。
剛體的定向 :描述剛體定向的方法有好幾種,包括方向餘弦 、歐拉角 、四元數 等等。這些方法設定一個附體參考系B的定向(相對於空間參考系S)。附體參考系是固定於剛體的參考系。相對於剛體,附體參考系的定向固定不變。由於剛體可能會呈加速度運動,所以附體參考系可能不是慣性參考系。空間參考系是某設定慣性參考系,例如,在觀測飛機的飛行運動時,附著於飛機場控制塔 的參考系可以設定為空間參考系,而附著於飛機的參考系則可設定為附體參考系。剛體的定向 需要用到另外三個自由度。
方向餘弦 方法可以用來設定,附體參考系B的定向,從而設定剛體的定向。假設沿著參考系S的坐標軸的三個單位向量分別為
x
^
1
{\displaystyle {\hat {\mathbf {x} }}_{1}}
x
^
2
{\displaystyle {\hat {\mathbf {x} }}_{2}}
x
^
3
{\displaystyle {\hat {\mathbf {x} }}_{3}}
e
^
1
{\displaystyle {\hat {\mathbf {e} }}_{1}}
e
^
2
{\displaystyle {\hat {\mathbf {e} }}_{2}}
e
^
3
{\displaystyle {\hat {\mathbf {e} }}_{3}}
e
^
i
{\displaystyle {\hat {\mathbf {e} }}_{i}}
x
^
j
{\displaystyle {\hat {\mathbf {x} }}_{j}}
a
i
j
{\displaystyle a_{ij}}
a
i
j
=
d
e
f
cos
(
θ
i
j
)
{\displaystyle a_{ij}\ {\stackrel {def}{=}}\ \cos {(\theta _{ij})}}
其中,
θ
i
j
{\displaystyle \theta _{ij}}
e
^
i
{\displaystyle {\hat {\mathbf {e} }}_{i}}
x
^
j
{\displaystyle {\hat {\mathbf {x} }}_{j}}
e
^
1
{\displaystyle {\hat {\mathbf {e} }}_{1}}
e
^
2
{\displaystyle {\hat {\mathbf {e} }}_{2}}
e
^
3
{\displaystyle {\hat {\mathbf {e} }}_{3}}
x
^
1
{\displaystyle {\hat {\mathbf {x} }}_{1}}
x
^
2
{\displaystyle {\hat {\mathbf {x} }}_{2}}
x
^
3
{\displaystyle {\hat {\mathbf {x} }}_{3}}
e
^
1
=
cos
(
θ
11
)
x
^
1
+
cos
(
θ
12
)
x
^
2
+
cos
(
θ
13
)
x
^
3
=
a
11
x
^
1
+
a
12
x
^
2
+
a
13
x
^
3
{\displaystyle {\hat {\mathbf {e} }}_{1}=\cos {(\theta _{11})}{\hat {\mathbf {x} }}_{1}+\cos {(\theta _{12})}{\hat {\mathbf {x} }}_{2}+\cos {(\theta _{13})}{\hat {\mathbf {x} }}_{3}=a_{11}{\hat {\mathbf {x} }}_{1}+a_{12}{\hat {\mathbf {x} }}_{2}+a_{13}{\hat {\mathbf {x} }}_{3}}
e
^
2
=
cos
(
θ
21
)
x
^
1
+
cos
(
θ
22
)
x
^
2
+
cos
(
θ
23
)
x
^
3
=
a
21
x
^
1
+
a
22
x
^
2
+
a
23
x
^
3
{\displaystyle {\hat {\mathbf {e} }}_{2}=\cos {(\theta _{21})}{\hat {\mathbf {x} }}_{1}+\cos {(\theta _{22})}{\hat {\mathbf {x} }}_{2}+\cos {(\theta _{23})}{\hat {\mathbf {x} }}_{3}=a_{21}{\hat {\mathbf {x} }}_{1}+a_{22}{\hat {\mathbf {x} }}_{2}+a_{23}{\hat {\mathbf {x} }}_{3}}
e
^
3
=
cos
(
θ
31
)
x
^
1
+
cos
(
θ
32
)
x
^
2
+
cos
(
θ
33
)
x
^
3
=
a
31
x
^
1
+
a
32
x
^
2
+
a
33
x
^
3
{\displaystyle {\hat {\mathbf {e} }}_{3}=\cos {(\theta _{31})}{\hat {\mathbf {x} }}_{1}+\cos {(\theta _{32})}{\hat {\mathbf {x} }}_{2}+\cos {(\theta _{33})}{\hat {\mathbf {x} }}_{3}=a_{31}{\hat {\mathbf {x} }}_{1}+a_{32}{\hat {\mathbf {x} }}_{2}+a_{33}{\hat {\mathbf {x} }}_{3}}
兩個參考系的坐標軸所形成的矩陣 稱為「方向餘弦矩陣」
A
{\displaystyle A}
A
=
[
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
]
{\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}}}
採用愛因斯坦求和約定 ,由於
e
^
i
=
a
i
j
x
^
j
{\displaystyle {\hat {\mathbf {e} }}_{i}=a_{ij}{\hat {\mathbf {x} }}_{j}}
A
{\displaystyle A}
反過來,經過一番運算,可以得到
x
^
j
=
a
i
j
e
^
i
{\displaystyle {\hat {\mathbf {x} }}_{j}=a_{ij}{\hat {\mathbf {e} }}_{i}}
給定位置向量
r
{\displaystyle \mathbf {r} }
r
=
x
1
x
^
1
+
x
2
x
^
2
+
x
3
x
^
3
=
e
1
e
^
1
+
e
2
e
^
2
+
e
3
e
^
3
{\displaystyle \mathbf {r} =x_{1}{\hat {\mathbf {x} }}_{1}+x_{2}{\hat {\mathbf {x} }}_{2}+x_{3}{\hat {\mathbf {x} }}_{3}=e_{1}{\hat {\mathbf {e} }}_{1}+e_{2}{\hat {\mathbf {e} }}_{2}+e_{3}{\hat {\mathbf {e} }}_{3}}
則
r
{\displaystyle \mathbf {r} }
e
^
i
{\displaystyle {\hat {\mathbf {e} }}_{i}}
內積 為
r
e
^
˙
i
=
e
i
=
a
i
1
x
1
+
a
i
2
x
2
+
a
i
3
x
3
=
a
i
j
x
j
{\displaystyle \mathbf {r} {\dot {\hat {\mathbf {e} }}}_{i}=e_{i}=a_{i1}x_{1}+a_{i2}x_{2}+a_{i3}x_{3}=a_{ij}x_{j}}
方向餘弦矩陣
A
{\displaystyle A}
(
x
1
,
x
2
,
x
3
)
{\displaystyle (x_{1},x_{2},x_{3})}
(
e
1
,
e
2
,
e
3
)
{\displaystyle (e_{1},e_{2},e_{3})}
變換矩陣
A
{\displaystyle A}
x
j
=
a
i
j
e
i
{\displaystyle x_{j}=a_{ij}e_{i}}
變換矩陣
A
{\displaystyle A}
正交矩陣 ,滿足「正交條件」
a
i
j
a
i
k
=
δ
j
k
{\displaystyle a_{ij}a_{ik}=\delta _{jk}}
其中,
δ
j
k
{\displaystyle \delta _{jk}}
克羅內克函數 。
注意到
θ
i
j
{\displaystyle \theta _{ij}}
θ
j
i
{\displaystyle \theta _{ji}}
θ
j
i
{\displaystyle \theta _{ji}}
e
^
j
{\displaystyle {\hat {\mathbf {e} }}_{j}}
x
^
i
{\displaystyle {\hat {\mathbf {x} }}_{i}}
A
{\displaystyle A}
對稱矩陣 。
左圖顯示「主動變換」:參考軸不變,點P被旋轉角弧
−
θ
{\displaystyle -\theta }
θ
{\displaystyle \theta }
對於二維旋轉 ,變換矩陣
A
{\displaystyle A}
旋轉矩陣 。例如,將附體參考系B或剛體旋轉,從
e
^
1
{\displaystyle {\hat {\mathbf {e} }}_{1}}
e
^
2
{\displaystyle {\hat {\mathbf {e} }}_{2}}
e
^
3
{\displaystyle {\hat {\mathbf {e} }}_{3}}
θ
{\displaystyle \theta }
e
^
1
′
{\displaystyle {\hat {\mathbf {e} }}'_{1}}
e
^
2
′
{\displaystyle {\hat {\mathbf {e} }}'_{2}}
e
^
3
′
{\displaystyle {\hat {\mathbf {e} }}'_{3}}
e
^
3
=
e
^
3
′
{\displaystyle {\hat {\mathbf {e} }}_{3}={\hat {\mathbf {e} }}'_{3}}
A
{\displaystyle A}
A
=
[
cos
θ
sin
θ
0
−
sin
θ
cos
θ
0
0
0
1
]
{\displaystyle A={\begin{bmatrix}\cos {\theta }&\sin {\theta }&0\\-\sin {\theta }&\cos {\theta }&0\\0&0&1\end{bmatrix}}}
參考軸
e
^
i
′
{\displaystyle {\hat {\mathbf {e} }}'_{i}}
e
^
j
{\displaystyle {\hat {\mathbf {e} }}_{j}}
e
^
i
′
=
a
i
j
e
^
j
{\displaystyle {\hat {\mathbf {e} }}'_{i}=a_{ij}{\hat {\mathbf {e} }}_{j}}
換一方面,旋轉矩陣
A
{\displaystyle A}
r
=
x
i
x
^
i
{\displaystyle \mathbf {r} =x_{i}{\hat {\mathbf {x} }}_{i}}
−
θ
{\displaystyle -\theta }
r
′
=
x
i
′
x
^
i
{\displaystyle \mathbf {r} '=x'_{i}{\hat {\mathbf {x} }}_{i}}
x
i
′
=
a
i
j
x
j
{\displaystyle x'_{i}=a_{ij}x_{j}}
按照順序使用最多三個歐拉角 (
α
,
β
,
γ
{\displaystyle \alpha ,\ \beta ,\ \gamma }
方向餘弦矩陣
A
{\displaystyle A}
A
{\displaystyle A}
自變量 (independent variable ))。歐拉角的三個自變量可以用來設定剛體的定向。
相對於空間參考系S,附體參考系B的定向,可以用三個歐拉角來設定。參閱右圖。設定 xyz-軸為空間參考系S的坐標軸,XYZ-軸為附體參考系B的坐標軸。稱 xy-平面與 XY-平面的相交為交點線 ,用英文字母(N)代表。按照「zxz 順規」,歐拉角可以這樣定義:
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
γ
{\displaystyle \gamma }
每一個歐拉角的旋轉都對應於一個簡單的旋轉矩陣:
A
α
=
[
cos
α
sin
α
0
−
sin
α
cos
α
0
0
0
1
]
{\displaystyle A_{\alpha }={\begin{bmatrix}\cos \alpha &\sin \alpha &0\\-\sin \alpha &\cos \alpha &0\\0&0&1\end{bmatrix}}}
、
A
β
=
[
1
0
0
0
cos
β
sin
β
0
−
sin
β
cos
β
]
{\displaystyle A_{\beta }={\begin{bmatrix}1&0&0\\0&\cos \beta &\sin \beta \\0&-\sin \beta &\cos \beta \end{bmatrix}}}
、
A
γ
=
[
cos
γ
sin
γ
0
−
sin
γ
cos
γ
0
0
0
1
]
{\displaystyle A_{\gamma }={\begin{bmatrix}\cos \gamma &\sin \gamma &0\\-\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}}
。 設定剛體定向的旋轉矩陣
A
{\displaystyle A}
A
α
{\displaystyle A_{\alpha }}
A
β
{\displaystyle A_{\beta }}
A
γ
{\displaystyle A_{\gamma }}
A
=
A
γ
A
β
A
α
{\displaystyle A=A_{\gamma }A_{\beta }A_{\alpha }}
單獨分開工作,每個矩陣各自代表一種旋轉。按照順序相乘,
最裏面的(最右的)矩陣代表繞著 z 軸的旋轉。
最外面的(最左的)矩陣代表繞著 Z 軸的旋轉。
在中間的矩陣代表繞著交點線的旋轉。 經過一番運算,可以得到
A
{\displaystyle A}
A
=
[
cos
α
cos
γ
−
cos
β
sin
α
sin
γ
sin
α
cos
γ
+
cos
β
cos
α
sin
γ
sin
β
sin
γ
−
cos
α
sin
γ
−
cos
β
sin
α
cos
γ
−
sin
α
sin
γ
+
cos
β
cos
α
cos
γ
sin
β
cos
γ
sin
β
sin
α
−
sin
β
cos
α
cos
β
]
{\displaystyle A={\begin{bmatrix}\cos \alpha \cos \gamma -\cos \beta \sin \alpha \sin \gamma &\sin \alpha \cos \gamma +\cos \beta \cos \alpha \sin \gamma &\sin \beta \sin \gamma \\-\cos \alpha \sin \gamma -\cos \beta \sin \alpha \cos \gamma &-\sin \alpha \sin \gamma +\cos \beta \cos \alpha \cos \gamma &\sin \beta \cos \gamma \\\sin \beta \sin \alpha &-\sin \beta \cos \alpha &\cos \beta \end{bmatrix}}}
。
A
{\displaystyle A}
逆矩陣 是:
A
−
1
=
[
cos
α
cos
γ
−
cos
β
sin
α
sin
γ
−
cos
α
sin
γ
−
cos
β
sin
α
cos
γ
sin
β
sin
α
sin
α
cos
γ
+
cos
β
cos
α
sin
γ
−
sin
α
sin
γ
+
cos
β
cos
α
cos
γ
−
sin
β
cos
α
sin
β
sin
γ
sin
β
cos
γ
cos
β
]
{\displaystyle A^{-1}={\begin{bmatrix}\cos \alpha \cos \gamma -\cos \beta \sin \alpha \sin \gamma &-\cos \alpha \sin \gamma -\cos \beta \sin \alpha \cos \gamma &\sin \beta \sin \alpha \\\sin \alpha \cos \gamma +\cos \beta \cos \alpha \sin \gamma &-\sin \alpha \sin \gamma +\cos \beta \cos \alpha \cos \gamma &-\sin \beta \cos \alpha \\\sin \beta \sin \gamma &\sin \beta \cos \gamma &\cos \beta \end{bmatrix}}}
。
歐拉旋轉定理 表明,在三維空間裏,假設約束剛體內部一點固定不動,則其任意位移等價於繞著某固定軸的一個旋轉,而這固定軸必含有這固定點。換句話說,設定附體參考系B的原點為這固定點,則附體參考系B不會因為這位移而涉及任何平移運動,再設定附體參考系B的z-軸與固定軸同軸,則這位移對應於繞著附體參考系B的z-軸旋轉
γ
{\displaystyle \gamma }
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
[ 2]
改變剛體的定向與旋轉其附體參考系相同。 對於內部有一點被約束固定不動的剛體(或原點固定不動的參考系),歐拉旋轉定理將其任意位移等價為繞著某固定軸的一個旋轉。這允許使用旋轉來表達定向的改變。因此,變換矩陣
A
{\displaystyle A}
三維旋轉 的旋轉矩陣 ,將附體參考系B或剛體做任意環繞著固定點的旋轉,從
e
^
1
{\displaystyle {\hat {\mathbf {e} }}_{1}}
e
^
2
{\displaystyle {\hat {\mathbf {e} }}_{2}}
e
^
3
{\displaystyle {\hat {\mathbf {e} }}_{3}}
e
^
1
′
{\displaystyle {\hat {\mathbf {e} }}'_{1}}
e
^
2
′
{\displaystyle {\hat {\mathbf {e} }}'_{2}}
e
^
3
′
{\displaystyle {\hat {\mathbf {e} }}'_{3}}
e
^
i
′
{\displaystyle {\hat {\mathbf {e} }}'_{i}}
e
^
j
{\displaystyle {\hat {\mathbf {e} }}_{j}}
e
^
i
′
=
a
i
j
e
^
j
{\displaystyle {\hat {\mathbf {e} }}'_{i}=a_{ij}{\hat {\mathbf {e} }}_{j}}
當剛體移動時,它的位置與定向都可能會隨著時間演進而改變。在運動學 裏,這可分為平移運動與旋轉運動。根據沙勒定理 (Chasles' theorem ),歐拉旋轉定律的推論 ,剛體的最廣義位移等價於一個平移加上一個旋轉。[ 2]
r
P
{\displaystyle \mathbf {r} _{P}}
r
P
=
r
G
+
r
P
/
G
{\displaystyle \mathbf {r} _{P}=\mathbf {r} _{G}+\mathbf {r} _{P/G}}
其中,
r
G
{\displaystyle \mathbf {r} _{G}}
r
P
/
G
{\displaystyle \mathbf {r} _{P/G}}
從附體參考系B觀測,剛體內部每一點的位置都固定不變。剛體從時間
t
0
{\displaystyle t_{0}}
t
{\displaystyle t}
r
G
(
t
0
)
{\displaystyle \mathbf {r} _{G}(t_{0})}
r
G
(
t
)
{\displaystyle \mathbf {r} _{G}(t)}
r
P
/
G
{\displaystyle \mathbf {r} _{P/G}}
t
0
{\displaystyle t_{0}}
t
{\displaystyle t}
從不同的參考系觀測剛體運動,可能會獲得不同的平移速度和不同的角速度。為了確保測量結果具有實際物理意義,必需先給定參考系。
剛體的平移速度是向量,是其位置向量的時間變化率,是附著於剛體的附體參考系的原點的速度。對於純平移運動(沒有任何旋轉運動),剛體內部所有點的移動速度相同。假設涉及旋轉運動,則通常剛體內部任意兩點的瞬時速度不相等;只有當它們恰巧處於同一直軸,而這直軸平行於轉動瞬軸 (instantaneous axis of rotation ),則它們的瞬時速度相等。
角速度也是向量,描述剛體定向改變的角速率,以及剛體旋轉時的瞬時轉軸(歐拉旋轉定理 保證瞬時轉軸的存在)。在任意時間,剛體內部每一個粒子的角速度相同。
假設一剛體呈純旋轉運動,其附體參考系B也會跟著旋轉,因此,對於任意向量
F
{\displaystyle \mathbf {F} }
(
e
^
1
,
e
^
2
,
e
^
3
)
{\displaystyle ({\hat {\mathbf {e} }}_{1},{\hat {\mathbf {e} }}_{2},{\hat {\mathbf {e} }}_{3})}
(
x
^
1
,
x
^
2
,
x
^
3
)
{\displaystyle ({\hat {\mathbf {x} }}_{1},{\hat {\mathbf {x} }}_{2},{\hat {\mathbf {x} }}_{3})}
F
(
t
)
{\displaystyle \mathbf {F} (t)}
F
=
f
i
x
^
i
=
F
i
e
^
i
{\displaystyle \mathbf {F} =f_{i}{\hat {\mathbf {x} }}_{i}=F_{i}{\hat {\mathbf {e} }}_{i}}
F
(
t
)
{\displaystyle \mathbf {F} (t)}
d
F
d
t
=
d
f
i
d
t
x
^
i
=
d
F
i
d
t
e
^
i
+
F
i
d
e
^
i
d
t
{\displaystyle {\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}={\frac {\mathrm {d} f_{i}}{\mathrm {d} t}}{\hat {\mathbf {x} }}_{i}={\frac {\mathrm {d} F_{i}}{\mathrm {d} t}}{\hat {\mathbf {e} }}_{i}+F_{i}{\frac {\mathrm {d} {\hat {\mathbf {e} }}_{i}}{\mathrm {d} t}}}
單獨計算附體參考軸對於時間的導數:
d
e
^
i
d
t
=
d
d
t
(
a
i
j
x
^
j
)
=
a
˙
i
j
x
^
j
=
a
˙
i
j
a
k
j
e
^
k
{\displaystyle {\frac {\mathrm {d} {\hat {\mathbf {e} }}_{i}}{\mathrm {d} t}}={\frac {\mathrm {d} }{\mathrm {d} t}}(a_{ij}{\hat {\mathbf {x} }}_{j})={\dot {a}}_{ij}{\hat {\mathbf {x} }}_{j}={\dot {a}}_{ij}a_{kj}{\hat {\mathbf {e} }}_{k}}
其中,
a
˙
i
j
=
d
e
f
d
d
t
a
i
j
{\displaystyle {\dot {a}}_{ij}\ {\stackrel {def}{=}}\ {\frac {\mathrm {d} }{\mathrm {d} t}}a_{ij}}
由於
d
d
t
e
^
i
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\hat {\mathbf {e} }}_{i}}
e
^
i
{\displaystyle {\hat {\mathbf {e} }}_{i}}
d
d
t
e
^
i
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\hat {\mathbf {e} }}_{i}}
線性組合 :
d
d
t
e
^
i
=
−
ϵ
i
j
ℓ
ω
i
j
e
^
ℓ
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\hat {\mathbf {e} }}_{i}=-\epsilon _{ij\ell }\omega _{ij}{\hat {\mathbf {e} }}_{\ell }}
其中,
ϵ
i
j
ℓ
{\displaystyle \epsilon _{ij\ell }}
列維-奇維塔符號 ,
ω
i
j
{\displaystyle \omega _{ij}}
對於任意
e
^
m
≠
e
^
i
{\displaystyle {\hat {\mathbf {e} }}_{m}\neq {\hat {\mathbf {e} }}_{i}}
e
^
i
{\displaystyle {\hat {\mathbf {e} }}_{i}}
e
^
m
{\displaystyle {\hat {\mathbf {e} }}_{m}}
d
d
t
(
e
^
i
⋅
e
^
m
)
=
(
d
d
t
e
^
i
)
⋅
e
^
m
+
e
^
i
⋅
(
d
d
t
e
^
m
)
=
−
ϵ
i
j
ℓ
ω
i
j
e
^
ℓ
⋅
e
^
m
−
e
^
i
⋅
ϵ
m
j
ℓ
ω
m
j
e
^
ℓ
=
−
ϵ
i
j
m
ω
i
j
−
ϵ
m
j
i
ω
m
j
=
−
ϵ
i
j
m
(
ω
i
j
−
ω
m
j
)
=
0
{\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} t}}({\hat {\mathbf {e} }}_{i}\cdot {\hat {\mathbf {e} }}_{m})&=\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\hat {\mathbf {e} }}_{i}\right)\cdot {\hat {\mathbf {e} }}_{m}+{\hat {\mathbf {e} }}_{i}\cdot \left({\frac {\mathrm {d} }{\mathrm {d} t}}{\hat {\mathbf {e} }}_{m}\right)\\&=-\epsilon _{ij\ell }\omega _{ij}{\hat {\mathbf {e} }}_{\ell }\cdot {\hat {\mathbf {e} }}_{m}-{\hat {\mathbf {e} }}_{i}\cdot \epsilon _{mj\ell }\omega _{mj}{\hat {\mathbf {e} }}_{\ell }\\&=-\epsilon _{ijm}\omega _{ij}-\epsilon _{mji}\omega _{mj}\\&=-\epsilon _{ijm}(\omega _{ij}-\omega _{mj})\\&=0\\\end{aligned}}}
所以,
ω
i
j
{\displaystyle \omega _{ij}}
i
{\displaystyle i}
ω
j
{\displaystyle \omega _{j}}
d
d
t
e
^
i
=
−
ϵ
i
j
ℓ
ω
j
e
^
ℓ
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\hat {\mathbf {e} }}_{i}=-\epsilon _{ij\ell }\omega _{j}{\hat {\mathbf {e} }}_{\ell }}
思考
d
F
d
t
{\displaystyle {\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}}
F
i
d
e
^
i
d
t
{\displaystyle F_{i}{\frac {\mathrm {d} {\hat {\mathbf {e} }}_{i}}{\mathrm {d} t}}}
i
{\displaystyle i}
ℓ
{\displaystyle \ell }
F
i
d
e
^
i
d
t
=
−
ϵ
i
j
ℓ
F
i
ω
j
e
^
ℓ
=
ϵ
i
j
ℓ
e
^
i
ω
j
F
ℓ
=
ω
×
F
{\displaystyle F_{i}{\frac {\mathrm {d} {\hat {\mathbf {e} }}_{i}}{\mathrm {d} t}}=-\epsilon _{ij\ell }F_{i}\omega _{j}{\hat {\mathbf {e} }}_{\ell }=\epsilon _{ij\ell }{\hat {\mathbf {e} }}_{i}\omega _{j}F_{\ell }={\boldsymbol {\omega }}\times \mathbf {F} }
向量
ω
{\displaystyle {\boldsymbol {\omega }}}
ω
1
{\displaystyle \omega _{1}}
ω
2
{\displaystyle \omega _{2}}
ω
3
{\displaystyle \omega _{3}}
e
^
1
{\displaystyle {\hat {\mathbf {e} }}_{1}}
e
^
2
{\displaystyle {\hat {\mathbf {e} }}_{2}}
e
^
3
{\displaystyle {\hat {\mathbf {e} }}_{3}}
ω
1
=
a
˙
2
j
a
3
j
=
α
˙
sin
β
sin
γ
+
β
˙
cos
γ
{\displaystyle \omega _{1}={\dot {a}}_{2j}a_{3j}={\dot {\alpha }}\sin {\beta }\sin {\gamma }+{\dot {\beta }}\cos {\gamma }}
ω
2
=
−
a
˙
1
j
a
3
j
=
α
˙
sin
β
cos
γ
+
β
˙
sin
γ
{\displaystyle \omega _{2}=-{\dot {a}}_{1j}a_{3j}={\dot {\alpha }}\sin {\beta }\cos {\gamma }+{\dot {\beta }}\sin {\gamma }}
ω
3
=
a
˙
1
j
a
2
j
=
α
˙
cos
β
+
γ
˙
{\displaystyle \omega _{3}={\dot {a}}_{1j}a_{2j}={\dot {\alpha }}\cos {\beta }+{\dot {\gamma }}}
試想對應於歐拉角
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
γ
{\displaystyle \gamma }
z
^
{\displaystyle {\hat {\mathbf {z} }}}
N
^
{\displaystyle {\hat {\mathbf {N} }}}
Z
^
{\displaystyle {\hat {\mathbf {Z} }}}
ω
α
=
α
˙
z
^
=
α
˙
sin
β
sin
γ
X
^
+
α
˙
sin
β
cos
γ
Y
^
+
α
˙
cos
β
Z
^
{\displaystyle {\boldsymbol {\omega }}_{\alpha }={\dot {\alpha }}{\hat {\mathbf {z} }}={\dot {\alpha }}\sin {\beta }\sin {\gamma }{\hat {\mathbf {X} }}+{\dot {\alpha }}\sin {\beta }\cos {\gamma }{\hat {\mathbf {Y} }}+{\dot {\alpha }}\cos {\beta }{\hat {\mathbf {Z} }}}
ω
β
=
β
˙
N
^
=
β
˙
cos
γ
X
^
−
β
˙
sin
γ
Y
^
{\displaystyle {\boldsymbol {\omega }}_{\beta }={\dot {\beta }}{\hat {\mathbf {N} }}={\dot {\beta }}\cos {\gamma }{\hat {\mathbf {X} }}-{\dot {\beta }}\sin {\gamma }{\hat {\mathbf {Y} }}}
ω
γ
=
γ
˙
Z
^
{\displaystyle {\boldsymbol {\omega }}_{\gamma }={\dot {\gamma }}{\hat {\mathbf {Z} }}}
這三個角速度的向量和,對於附體參考系B的分量分別為
ω
X
=
α
˙
sin
β
sin
γ
+
β
˙
cos
γ
=
ω
1
{\displaystyle \omega _{X}={\dot {\alpha }}\sin {\beta }\sin {\gamma }+{\dot {\beta }}\cos {\gamma }=\omega _{1}}
ω
Y
=
α
˙
sin
β
cos
γ
+
β
˙
sin
γ
=
ω
2
{\displaystyle \omega _{Y}={\dot {\alpha }}\sin {\beta }\cos {\gamma }+{\dot {\beta }}\sin {\gamma }=\omega _{2}}
ω
Z
=
α
˙
cos
β
+
γ
˙
=
ω
3
{\displaystyle \omega _{Z}={\dot {\alpha }}\cos {\beta }+{\dot {\gamma }}=\omega _{3}}
注意到附體參考系B的
e
^
1
{\displaystyle {\hat {\mathbf {e} }}_{1}}
e
^
2
{\displaystyle {\hat {\mathbf {e} }}_{2}}
e
^
3
{\displaystyle {\hat {\mathbf {e} }}_{3}}
X
^
{\displaystyle {\hat {\mathbf {X} }}}
Y
^
{\displaystyle {\hat {\mathbf {Y} }}}
Z
^
{\displaystyle {\hat {\mathbf {Z} }}}
ω
{\displaystyle {\boldsymbol {\omega }}}
總結,向量
F
(
t
)
{\displaystyle \mathbf {F} (t)}
d
F
d
t
=
d
f
i
d
t
x
^
i
=
d
F
i
d
t
e
^
i
+
ω
×
F
{\displaystyle {\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}={\frac {\mathrm {d} f_{i}}{\mathrm {d} t}}{\hat {\mathbf {x} }}_{i}={\frac {\mathrm {d} F_{i}}{\mathrm {d} t}}{\hat {\mathbf {e} }}_{i}+{\boldsymbol {\omega }}\times \mathbf {F} }
設定
(
d
F
d
t
)
s
p
a
c
e
{\displaystyle \left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)_{\mathrm {space} }}
(
d
F
d
t
)
b
o
d
y
{\displaystyle \left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)_{\mathrm {body} }}
F
(
t
)
{\displaystyle \mathbf {F} (t)}
(
d
F
d
t
)
s
p
a
c
e
=
(
d
F
d
t
)
b
o
d
y
+
ω
×
F
{\displaystyle \left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)_{\mathrm {space} }=\left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)_{\mathrm {body} }+{\boldsymbol {\omega }}\times \mathbf {F} }
由於向量
F
(
t
)
{\displaystyle \mathbf {F} (t)}
(
d
d
t
)
s
p
a
c
e
{\displaystyle \left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)_{\mathrm {space} }}
(
d
d
t
)
b
o
d
y
{\displaystyle \left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)_{\mathrm {body} }}
(
d
d
t
)
s
p
a
c
e
=
(
d
d
t
)
b
o
d
y
+
ω
×
{\displaystyle \left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)_{\mathrm {space} }=\left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)_{\mathrm {body} }+{\boldsymbol {\omega }}\times }
這算符方程式可以作用於任意含時向量。
主项目:刚体动力学 描述刚体的平移运动(位置、速度、加速度等等),刚体内任意一点皆可被用为参考点(L参考系的原点)。但是,根据实际需要,一个适当的选择是:
整个刚体的质心 ;
平移运动是零,或可以简易研算的点。例如:在轴 或铰链 上、在万向接头 的中心等等。 当质心被选为参考点时:
刚体的动量 与刚体旋转运动 无关。在任何时间,动量 等于刚体的总质量乘以平移 速度 。
不论刚体平移运动为何,对于质心的角动量 皆等同。所以,在计算角动量时,可以忽略平移运动。在任何时间,角动量等于惯性张量 乘以角速度。假若知道刚体环绕于主轴 的角速度,那麼,对应于每一主轴的角动量,是对应的主慣性矩 乘以对应的角速度;力矩 是转动惯量乘以角加速度。
在无外力作用下,可能形成的运动为等速直线运动 、稳定绕固定轴旋转运动 、无力矩的进动 等等。
作用于刚体的净外力,等于总质量乘以刚体平移运动的加速度(也就是说,不论净外力矩是否为零,或这刚体是否在作旋转运动,牛頓第二運動定律 可以正确地应用于刚体平移运动,)。
总动能 是平移动能 与旋转动能 的总和。
刚体的转动定理:
M
=
I
α
{\displaystyle M=I\alpha \,\!}
M
{\displaystyle M\,\!}
I
{\displaystyle I\,\!}
α
{\displaystyle \alpha \,\!}
刚体的转动动能定理 :
W
=
∫
θ
1
θ
2
M
d
θ
=
1
2
I
ω
2
2
−
1
2
I
ω
1
2
{\displaystyle W=\int _{\theta _{1}}^{\theta _{2}}M\,d\theta ={\frac {1}{2}}I\omega _{2}^{2}-{\frac {1}{2}}I\omega _{1}^{2}\,\!}
∫
θ
1
θ
2
M
d
θ
{\displaystyle \int _{\theta _{1}}^{\theta _{2}}M\,d\theta \,\!}
M
{\displaystyle M\,\!}
θ
2
−
θ
1
{\displaystyle \theta _{2}-\theta _{1}\,\!}
I
{\displaystyle I\,\!}
ω
{\displaystyle \omega \,\!}
刚体的转动和平动可以合成为刚体的平面运动,由柯尼希定理 ,其动能为
E
k
=
1
2
m
V
c
2
+
1
2
I
ω
2
{\displaystyle E_{k}={\frac {1}{2}}mV_{c}^{2}+{\frac {1}{2}}I\omega ^{2}\,\!}
V
c
{\displaystyle V_{c}\,\!}
J.L. Meriam, L.G. Kraige, "Engineering Mechanics: Dynamics,"第三版,ISBN 0471592730 。